Separata (1) de Ecuaciones Dimensionales
Lic. Percy Víctor Cañote Fajardo
1. Deducir la ecuación dimensional de las siguientes magnitudes: 1- Velocidad; 2- aceleración; 3- fuerza; 4- constante de gravitación universal; 5- constante dieléctrica K; 6- número p; 7- razones trigonométricas (seno, coseno, tangente).
2. El tiempo que tarda un objeto en caer, en caída libre y sin rozamiento, puede depender de la masa del cuerpo, m, de la altura de caída, h, y de la aceleración de la gravedad, g. Encuentre la dependencia con dichas magnitudes.
3. Deducir utilizando el análisis dimensional los valores de n y m en las siguientes expresiones:
 Siendo a la aceleración de una partícula que describe un movimiento circular uniforme, k, una constante adimensional, r el radio de la circunferencia, v el módulo de la velocidad lineal en la primera expresión y T, el periodo de un péndulo simple, l, su longitud y g la aceleración gravitatoria en la segunda.
Siendo a la aceleración de una partícula que describe un movimiento circular uniforme, k, una constante adimensional, r el radio de la circunferencia, v el módulo de la velocidad lineal en la primera expresión y T, el periodo de un péndulo simple, l, su longitud y g la aceleración gravitatoria en la segunda.
4. Si se cumple la expresión . Siendo
. Siendo  intensidad de corriente eléctrica, ¿Qué dimensiones tendrá RC?
intensidad de corriente eléctrica, ¿Qué dimensiones tendrá RC?
5. Al calcular el trabajo, W, realizado por una fuerza encontramos la siguiente expresión.
 averiguar si es correcta.
averiguar si es correcta.
6. Tenemos dos expresiones: 1) y = y0 sen (w .t) y , donde y e yo son longitudes, t tiempo y w es frecuencia angular (inverso de tiempo). Explique cuál de las dos es incorrecta.
, donde y e yo son longitudes, t tiempo y w es frecuencia angular (inverso de tiempo). Explique cuál de las dos es incorrecta.
7. El potencial eléctrico producido por una carga puntual, q , en un punto situado a una distancia r de dicha caga se expresa así: Demuestre que la expresión, V=k.s.r donde s es una densidad superficial de carga (carga/superficie) puede ser cierta.
Demuestre que la expresión, V=k.s.r donde s es una densidad superficial de carga (carga/superficie) puede ser cierta.
8. Demuestre que la expresión  en la que V es una diferencia de potencial eléctrico y l y r son longitudes tiene algún error.
en la que V es una diferencia de potencial eléctrico y l y r son longitudes tiene algún error.
9. A partir de la ley de Coulomb  , determine las unidades SI de ε0.
, determine las unidades SI de ε0.
10. La potencia de una hélice impulsora de un barco es  , donde, w = velocidad angular, r = radio de la hélice, D, densidad del agua del mar. Halle x, y, z.
, donde, w = velocidad angular, r = radio de la hélice, D, densidad del agua del mar. Halle x, y, z.
11. De la ley de la atracción universal de las masas,  , halle la ecuación dimensional de K.
, halle la ecuación dimensional de K.
12. Fuerza centrípeta depende de la masa, la velocidad y del radio de giro del cuerpo en rotación. Halle la formula correcta para a fuerza centrípeta.
13. La formula de Bernoulli para medir la energía de un líquido que discurre es:

,donde h, altura; p, presión; ρ, densidad; v, velocidad; g, aceleración de la gravedad; w, peso. Verifique el principio de homogeneidad dimensional.
14. La formula de la energía potencial es:

. Halle la ecuación dimensional de k.
15. La ecuación

es la expresión de un proceso físico concreto. Halle la ecuación dimensional de D y de y, donde, A = aceleración, B =velocidad, F =fuerza y

.
16. La energía de un choque es

, donde,

. Verifique la homgeneidad dimensional.
17. Halle las dimensiones de x para que la expresión, 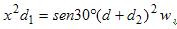 sea dimensionalmente correcta. Donde
sea dimensionalmente correcta. Donde  (aceleración angular) y w = velocidad angular.
(aceleración angular) y w = velocidad angular.
18. Determine x, y, z si la expresión dada es dimensionalmente correcta

, donde w = velocidad angular, t = Tiempo, d = longitud,

.
19. Un cuerpo se mueve y su trayectoria esta definida por

, donde x = distancia, v = velocidad,

. Determine las dimensiones de A.










 ,donde h, altura; p, presión; ρ, densidad; v, velocidad; g, aceleración de la gravedad; w, peso. Verifique el principio de homogeneidad dimensional.
,donde h, altura; p, presión; ρ, densidad; v, velocidad; g, aceleración de la gravedad; w, peso. Verifique el principio de homogeneidad dimensional. es la expresión de un proceso físico concreto. Halle la ecuación dimensional de D y de y, donde, A = aceleración, B =velocidad, F =fuerza y
es la expresión de un proceso físico concreto. Halle la ecuación dimensional de D y de y, donde, A = aceleración, B =velocidad, F =fuerza y .
.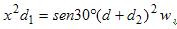

 , donde w = velocidad angular, t = Tiempo, d = longitud,
, donde w = velocidad angular, t = Tiempo, d = longitud,  .
. , donde x = distancia, v = velocidad,
, donde x = distancia, v = velocidad,  . Determine las dimensiones de A.
. Determine las dimensiones de A.








Publicar un comentario